在流体和磁流体系统中,不同扰动之间通过非线性相互作用产生湍流。湍动的能量可以在不同尺度之间传输,并在离子和电子尺度耗散。湍流的一个非常重要的特点是:存在多尺度的间歇性。空间间歇性表现为具有大梯度扰动的间歇结构。在普通流体中,其表现为涡丝等间歇结构。在磁流体中,间歇性表现为电流片、间断面、激波和阿尔芬涡等结构。现有的工作表明,湍动能量的耗散、等离子体的加速和热化主要发生在动力学尺度的间歇结构附近。然而,不同扰动量在不同尺度的间歇性特点,以及与间歇结构相关的湍动能量转移过程的具体物理机制仍然是待解决的问题。
近地空间充斥着大量的等离子体,是一个天然的等离子体实验室。太阳风和地磁层相互作用产生的磁鞘是宇宙中无碰撞等离子体激波下游的代表性区域。相比于太阳风,磁鞘通常具有较高的密度、温度、平均磁场强度和压缩性,以及等离子体β值。磁鞘中也大量存在着不稳定的动力学尺度波模以及相干结构。因此,在动力学尺度,磁鞘湍动不仅包括从大尺度串级而来的能量,也包括局地不稳定性直接注入的能量。由于目前对湍动间歇性的研究主要集中在太阳风中,同时考虑到上述太阳风和磁鞘的性质差异,磁鞘湍流的动力学尺度间歇性特点是一个值得注意及待解决的问题。
朱星宇、何建森等(2020)利用MMS卫星的高精度、高时间分辨率的磁场和电场数据,首次比较分析了七个磁鞘湍动事件离子尺度(~1Hz)到亚电子尺度(~1000Hz)磁场和电场的间歇性。这一工作研究了磁场和电场扰动的统计性质。同时,利用现有的湍流模型——Castaing模型,定量分析了磁场和电场统计性质的差异。
首先,他们分析了磁场和电场的单点概率密度分布。图1所示为其中一个事件的GSE坐标系下的三分量磁场和电场的时间序列和单点概率密度分布。
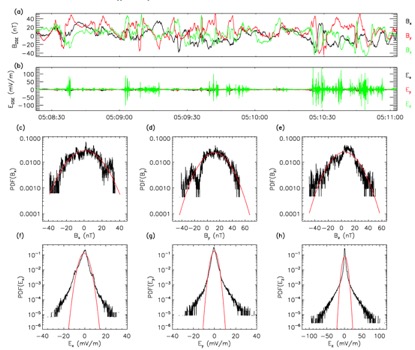
图1: (a&b)事件5的磁场、电场GSE坐标三分量时间序列;(c-h)磁场和电场在GSE坐标系下的三分量单点概率密度分布。红色实线为高斯拟合结果。
单点概率密度分布能够反映物理量的大尺度扰动的分布。由图1可以看出,磁场的分布非常接近高斯分布,而电场的分布则有一个非常高的尾部。这一“非高斯”的分布形态与电场时间序列上的尖峰有关。上述分析表明,电场在大尺度已经存在大梯度的扰动,其能量串级方式与磁场有显著差异。
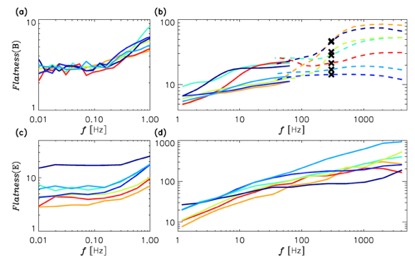
图2: 七个事件磁场(a&b)和电场(c&d)的平整度随尺度(f)的变化。
平整度可以用来定量诊断扰动的间歇性。平整度越大、平整度随尺度变化得越快,表明扰动的间歇性越强。图2展示的是这七个事件磁场(FB)和电场(FE)扰动平整度随尺度的变化。尺度大于5s时,FB都在3附近,FE在3-15之间,与尺度无关。尺度小于5s时,FE随尺度减小单调增加;FB基本随尺度的减小而增大(事件1,4,7在5-30Hz之间出现凸起),这一结果与太阳风中小于离子尺度的FB随尺度减小而减小不同。他们之间的一个明显差别是:FB在1000Hz左右不会超过100,而FE会超过100。
他们也比较了磁场和电场标度指数(ζ)与阶数(p)关系的差异,并首次给出了电场标度指数随阶数的变化,如图3所示。标度指数是通过对结构函数进行线性拟合得到的。磁场在电子惯性尺度(~30Hz)两侧的标度指数与阶数都成线性关系,表明其单分形的特点。而电场的标度指数先增加,在p=1-2之间达到最大值,然后随阶数的增加而减小。
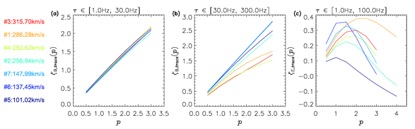
图3: 七个事件不同阶结构函数的标度指数(ζ)随阶数的变化(p)。
最后,他们利用描述不均匀湍动串级的Castaing模型(公式1)来定量分析磁场和电场间歇性的差异。其中,λ、μ为模型参数,μ为扰动量标准差的对数(lnσ)的最概然值,λ可以反应lnσ分布的展宽。图4所示为磁场和电场不同尺度(τ)的概率密度分布、Castaing模型的拟合结果及其拟合参数随尺度的变化。他们发现,对于磁场,对于电场
。
(1)
这一开创性的工作首次比较了磁鞘湍流亚离子尺度到亚电子尺度磁场和电场间歇性的差异。这一工作有助于解决动力学尺度湍动性质的问题,包括能量串级、压缩性等,为后续观测和理论研究提供观测依据及约束。这一工作发表在本领域著名的学术期刊《TheAstrophysicalJournal》上。
文章列表及链接:
X. Zhu, J. He, Y. Wang and L. Sorriso-Valvo, Difference of Intermittency between Electric Field and Magnetic Field Fluctuations from Ion Scale Down to Sub-electron Scale in the Magnetosheath Turbulence, 2020, ApJ, 893:124(11pp) (https://iopscience.iop.org/article/10.3847/1538-4357/ab7815)
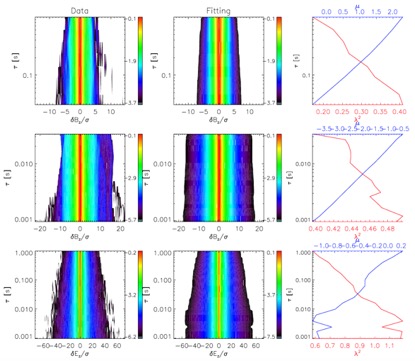
图4: (左)不同尺度磁场和电场扰动的概率密度分布;(中)Castaing模型拟合得到的概率密度分布;(右)模型拟合参数随尺度的变化。

